Occasionally, I come across descriptions of clustering or modeling techniques which include mention of "assumptions" being made by the algorithm. The "assumption" of normal errors from the linear model in least-squares regression is a good example. The "assumption" of Gaussian-distributed classes in discriminant analysis is another. I imagine that such assertions must leave novices with some questions and hesitation. What happens if these assumptions are not met? Can techniques ever be used if their assumptions are not tested and met? How badly can the assumption be broken before things go horribly wrong? It is important to understand the implications of these assumptions, and how they affect analysis.
In fact, the assumptions being made are made by the theorist who designed the algorithm, not the algorithm itself. Most often, such assumptions are necessary for some proof of optimality to hold. Considering myself the practical sort, I do not worry too much about these assumptions. What matters to me and my clients is how well the model works in practice (which can be assessed via test data), not how well its assumptions are met. Generally, such assumptions are rarely, if ever, strictly met in practice, and most of these algorithms do reasonably well even under such circumstances. A particular modeling algorithm may well be the best one available, despite not having its assumptions met.
My advice is to be aware of these assumptions to better understand the behavior of the algorithms one is using. Evaluate the performance of a specific modeling technique, not by looking back to its assumptions, but by looking forward to expected behavior, as indicated by rigorous out-of-sample and out-of-time testing.
Tips, tricks, and comments related to topics in data science and machine learning. Used to be called "data mining and predictive analytics" but updated the title to reflect the language of the day!
Hosted by Dean Abbott, Abbott Analytics
Saturday, April 25, 2009
Thursday, April 02, 2009
Why normalization matters with K-Means
A question about K-means clustering in Clementine was posted here. I thought I knew the answer, but took the opportunity to prove it to myself.
I took the KDD-Cup 98 data and just looked at four fields: Age, NumChild, TARGET_D (the amount the recaptured lapsed donors gave) and LASTGIFT. I took only four to make the problem simpler, and chose variables that had relatively large differences in mean values (where normalization might matter). Also, another problem with the two monetary variables is that they are both skewed positively (severely so).
The following image shows the results of two clustering runs: the first with raw data, the second with normalized data using the Clementine K-Means algorithm. The normalization consisted of log transforms (for TARGET_D and LASTGIFT) and z-scores for all (the log transformed fields, AGE and NUMCHILD). I used the default of 5 clusters.
Here are the results in tabular form. Note that I'm reporting unnormalized values for the "normalized" clusters even though the actual clusters were formed by the normalized values. This is purely for comparative purposes.
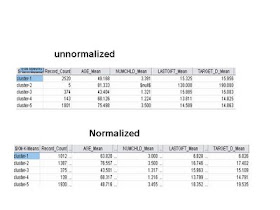
Note that:
1) the results are different, as measure by counts in each cluster
2) the unnormalized clusters are dominated by TARGET_D and LASTGIFT--one cluster contains the large values and the remaining have little variance.
3) AGE and NUMCHILD have some similar breakouts (40s with more children and 40s with fewer children for example).
So, the conclusion is (to answer the original question) K-Means in Clementine does not normalize the data. Since Euclidean distance is used, the clusters will be influenced strongly by the magnitudes of the variables, especially by outliers. Normalizing removes this bias. However, whether or not one desires this removal of bias depends on what one wants to find: sometimes if one would want a variable to influence the clusters more, one could manipulate the clusters precisely in this way, by increasing the relative magnitude of these fields.
One last issue that I didn't explore here, is the effects of correlated variables (LASTGIFT and TARGET_D to some degree here). It seems to me that correlated variables will artificially bias the clusters toward natural groupings of those variables, though I have never proved the extent of this bias in a controlled way (maybe someone can point to a paper that shows this clearly).
I took the KDD-Cup 98 data and just looked at four fields: Age, NumChild, TARGET_D (the amount the recaptured lapsed donors gave) and LASTGIFT. I took only four to make the problem simpler, and chose variables that had relatively large differences in mean values (where normalization might matter). Also, another problem with the two monetary variables is that they are both skewed positively (severely so).
The following image shows the results of two clustering runs: the first with raw data, the second with normalized data using the Clementine K-Means algorithm. The normalization consisted of log transforms (for TARGET_D and LASTGIFT) and z-scores for all (the log transformed fields, AGE and NUMCHILD). I used the default of 5 clusters.
Here are the results in tabular form. Note that I'm reporting unnormalized values for the "normalized" clusters even though the actual clusters were formed by the normalized values. This is purely for comparative purposes.

Note that:
1) the results are different, as measure by counts in each cluster
2) the unnormalized clusters are dominated by TARGET_D and LASTGIFT--one cluster contains the large values and the remaining have little variance.
3) AGE and NUMCHILD have some similar breakouts (40s with more children and 40s with fewer children for example).
So, the conclusion is (to answer the original question) K-Means in Clementine does not normalize the data. Since Euclidean distance is used, the clusters will be influenced strongly by the magnitudes of the variables, especially by outliers. Normalizing removes this bias. However, whether or not one desires this removal of bias depends on what one wants to find: sometimes if one would want a variable to influence the clusters more, one could manipulate the clusters precisely in this way, by increasing the relative magnitude of these fields.
One last issue that I didn't explore here, is the effects of correlated variables (LASTGIFT and TARGET_D to some degree here). It seems to me that correlated variables will artificially bias the clusters toward natural groupings of those variables, though I have never proved the extent of this bias in a controlled way (maybe someone can point to a paper that shows this clearly).
Wednesday, April 01, 2009
Graphing Considered Dangerous
In my posting of Jun-25-2007, To Graph Or Not To Graph , I made the case (tentatively) that graphs weren't all they're cracked up to be, and provoked some lively discussion in the Comments section here. In his Apr-01-2009 posting, Why tables are really much better than graphs on the Statistical Modeling, Causal Inference, and Social Science Web log, Andrew Gelman makes a much more forceful case against graphs. Readers may find Gelman's arguments of interest.
I am not "anti-graph", but do think that graphs are often used when other tools (test statistics, tables, etc.) would have been a better choice, and graphs are certainly frequently misused. Thoughts?
I am not "anti-graph", but do think that graphs are often used when other tools (test statistics, tables, etc.) would have been a better choice, and graphs are certainly frequently misused. Thoughts?